Estimating effect of multiple treatments

from dowhy import CausalModel
import dowhy.datasets

import warnings
warnings.filterwarnings('ignore')

data = dowhy.datasets.linear_dataset(10, num_common_causes=4, num_samples=10000,
                                     num_instruments=0, num_effect_modifiers=2,
                                     num_treatments=2,
                                     treatment_is_binary=False,
                                     num_discrete_common_causes=2,
                                     num_discrete_effect_modifiers=0,
                                     one_hot_encode=False)
df=data['df']
df.head()

	X0	X1	W0	W1	W2	W3	v0	v1	y
0	0.439382	-0.205453	2.529354	1.113537	2	0	13.771004	13.000752	472.597362
1	0.149839	-2.079429	-1.324029	-0.382790	2	3	20.099593	12.052128	-1533.635739
2	-1.274413	-0.251587	-1.933019	0.624964	0	0	-2.515991	-0.752427	-52.169030
3	-0.143148	0.981800	0.062478	0.157607	3	2	22.405199	16.950783	1669.945671
4	-0.518465	-2.574587	-0.364611	-0.051063	3	1	13.886915	14.532450	-2206.748459

model = CausalModel(data=data["df"],
                    treatment=data["treatment_name"], outcome=data["outcome_name"],
                    graph=data["gml_graph"])

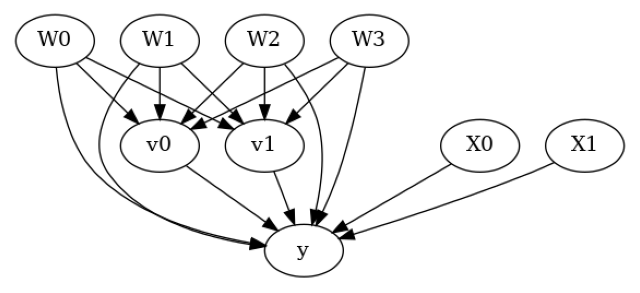
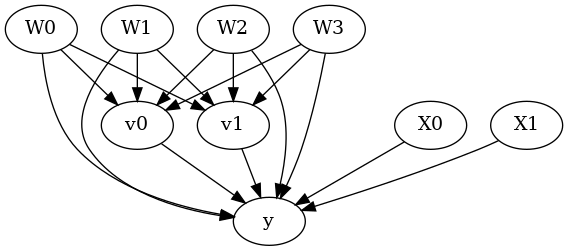
model.view_model()
from IPython.display import Image, display
display(Image(filename="causal_model.png"))

identified_estimand= model.identify_effect(proceed_when_unidentifiable=True)
print(identified_estimand)

Estimand type: EstimandType.NONPARAMETRIC_ATE

### Estimand : 1
Estimand name: backdoor
Estimand expression:
    d
─────────(E[y|W0,W1,W3,W2])
d[v₀  v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W0,W1,W3,W2,U) = P(y|v0,v1,W0,W1,W3,W2)

### Estimand : 2
Estimand name: iv
No such variable(s) found!

### Estimand : 3
Estimand name: frontdoor
No such variable(s) found!

Linear model

Let us first see an example for a linear model. The control_value and treatment_value can be provided as a tuple/list when the treatment is multi-dimensional.

The interpretation is change in y when v0 and v1 are changed from (0,0) to (1,1).

linear_estimate = model.estimate_effect(identified_estimand,
                                        method_name="backdoor.linear_regression",
                                        control_value=(0,0),
                                        treatment_value=(1,1),
                                        method_params={'need_conditional_estimates': False})
print(linear_estimate)

*** Causal Estimate ***

## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE

### Estimand : 1
Estimand name: backdoor
Estimand expression:
    d
─────────(E[y|W0,W1,W3,W2])
d[v₀  v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W0,W1,W3,W2,U) = P(y|v0,v1,W0,W1,W3,W2)

## Realized estimand
b: y~v0+v1+W0+W1+W3+W2+v0*X0+v0*X1+v1*X0+v1*X1
Target units: ate

## Estimate
Mean value: -100.73971170137605

You can estimate conditional effects, based on effect modifiers.

linear_estimate = model.estimate_effect(identified_estimand,
                                        method_name="backdoor.linear_regression",
                                        control_value=(0,0),
                                        treatment_value=(1,1))
print(linear_estimate)

*** Causal Estimate ***

## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE

### Estimand : 1
Estimand name: backdoor
Estimand expression:
    d
─────────(E[y|W0,W1,W3,W2])
d[v₀  v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W0,W1,W3,W2,U) = P(y|v0,v1,W0,W1,W3,W2)

## Realized estimand
b: y~v0+v1+W0+W1+W3+W2+v0*X0+v0*X1+v1*X0+v1*X1
Target units:

## Estimate
Mean value: -100.73971170137605
### Conditional Estimates
__categorical__X0             __categorical__X1
(-4.284000000000001, -1.409]  (-5.128, -1.633]    -283.778661
                              (-1.633, -1.053]    -227.693425
                              (-1.053, -0.525]    -195.630781
                              (-0.525, 0.0461]    -159.069413
                              (0.0461, 2.616]     -104.503596
(-1.409, -0.819]              (-5.128, -1.633]    -226.424752
                              (-1.633, -1.053]    -170.983067
                              (-1.053, -0.525]    -135.112545
                              (-0.525, 0.0461]    -102.557610
                              (0.0461, 2.616]      -43.652254
(-0.819, -0.329]              (-5.128, -1.633]    -191.453361
                              (-1.633, -1.053]    -135.394258
                              (-1.053, -0.525]    -100.786258
                              (-0.525, 0.0461]     -65.979753
                              (0.0461, 2.616]       -9.941882
(-0.329, 0.276]               (-5.128, -1.633]    -156.472730
                              (-1.633, -1.053]    -100.336103
                              (-1.053, -0.525]     -63.620204
                              (-0.525, 0.0461]     -31.116636
                              (0.0461, 2.616]       25.088725
(0.276, 3.165]                (-5.128, -1.633]     -99.093020
                              (-1.633, -1.053]     -43.450080
                              (-1.053, -0.525]      -4.915625
                              (-0.525, 0.0461]      26.443889
                              (0.0461, 2.616]       82.101963
dtype: float64

More methods

You can also use methods from EconML or CausalML libraries that support multiple treatments. You can look at examples from the conditional effect notebook: https://py-why.github.io/dowhy/example_notebooks/dowhy-conditional-treatment-effects.html

Propensity-based methods do not support multiple treatments currently.