On PAGs and their validity

A PAG or a Partial Ancestral Graph is a type of mixed edge graph that can represent, in a single graph, the causal relationship between several nodes as defined by an equivalence class of MAGs.

PAGs account for possible unobserved confounding and selection bias in the underlying equivalence class of SCMs.

Another way to understand this is that PAGs encode conditional independence constraints stemming from Causal Graphs. Since these constraints do not lead to a unique graph, a PAG, in essence, represents a class of graphs that encode the same conditional independence constraints.

PAGs model this relationship by displaying all common edge marks (tail and arrowhead) shared by all members in the equivalence class and displaying circle endpoints for those marks that are not common. That is, a circular endpoint (*-o) can represent both a directed (*->) and tail (*—) endpoint in causal graphs within the equivalence class.

More details on PAGs can be found at [1].

import pywhy_graphs
from pywhy_graphs.viz import draw
from pywhy_graphs import PAG

try:
    from dodiscover import FCI, make_context
    from dodiscover.ci import Oracle
    from dodiscover.constraint.utils import dummy_sample
except ImportError as e:
    raise ImportError("The 'dodiscover' package is required to convert a MAG to a PAG.")

PAGs in pywhy-graphs

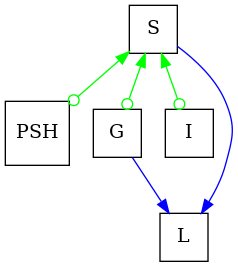
Constructing a PAG in pywhy-graphs is an easy task since the library provides a separate class for this purpose. True to the definition of PAGs, the class can contain directed edges, bidirected edges, undirected edges and cicle edges. To illustrate this, we construct an example PAG as described in [1], figure 4:

pag = PAG()
pag.add_edge("I", "S", pag.directed_edge_name)
pag.add_edge("G", "S", pag.directed_edge_name)
pag.add_edge("G", "L", pag.directed_edge_name)
pag.add_edge("S", "L", pag.directed_edge_name)
pag.add_edge("PSH", "S", pag.directed_edge_name)
pag.add_edge("S", "PSH", pag.circle_edge_name)
pag.add_edge("S", "G", pag.circle_edge_name)
pag.add_edge("S", "I", pag.circle_edge_name)


# Finally, the graph looks like this:
dot_graph = draw(pag)
dot_graph.render(outfile="valid_pag.png", view=True)

'valid_pag.png'

Validity of a PAG

For a PAG to be valid, it must represent a valid equivalent class of MAGs. This can be verified by turning the PAG into an MAG and then checking the validity of the MAG. Theorem 2 in [1] provides a method for checking the validity of a PAG. To check if the constructed PAG is a valid one in pywhy-graphs, we can simply do:

# returns True
print(pywhy_graphs.valid_pag(pag))

ConditioningSetSelection.PDS
Context(observed_variables={'S', 'G', 'I', 'L', 'PSH'}, latent_variables=set(), state_variables={}, init_graph=<networkx.classes.graph.Graph object at 0x7f2694fef250>, included_edges=<networkx.classes.graph.Graph object at 0x7f2694fef950>, excluded_edges=<networkx.classes.graph.Graph object at 0x7f2694fefd90>, num_distributions=1, obs_distribution=True, intervention_targets=[], symmetric_diff_map={}, sigma_map={}, f_nodes=[], num_domains=1, domain_map={}, s_nodes=[])
True

If we want to test whether this algorithm is working correctly or not, we can change a single mark in the graph such that the PAG. By removing a circle edge, we are removing the representation of multiple marks as encoded by the different MAGs this PAG represents. In this specific case, by removing the circle endpoint S *-o I, we are saying that S directly causes I. However, there is no way of determining this using the FCI logical rules. One would not be able to determine that the adjacency is due to a direct causal relationship (directed edge), confounded relationship (bidirected edge), or an inducing path relationship. As such, the resulting graph is no longer a valid PAG.

pag.remove_edge("S", "I", pag.circle_edge_name)

# returns False
print(pywhy_graphs.valid_pag(pag))

ConditioningSetSelection.PDS
Context(observed_variables={'S', 'G', 'I', 'L', 'PSH'}, latent_variables=set(), state_variables={}, init_graph=<networkx.classes.graph.Graph object at 0x7f2694fcefd0>, included_edges=<networkx.classes.graph.Graph object at 0x7f2694e17ed0>, excluded_edges=<networkx.classes.graph.Graph object at 0x7f2694e16750>, num_distributions=1, obs_distribution=True, intervention_targets=[], symmetric_diff_map={}, sigma_map={}, f_nodes=[], num_domains=1, domain_map={}, s_nodes=[])
False

References

[1] (1,2,3)

Jiji Zhang. On the completeness of orientation rules for causal discovery in the presence of latent confounders and selection bias. Artificial Intelligence, 172(16):1873–1896, 2008. URL: https://www.sciencedirect.com/science/article/pii/S0004370208001008, doi:https://doi.org/10.1016/j.artint.2008.08.001.

Estimated memory usage: 168 MB