An introduction to Inducing Paths and how to find them

A path p is called an inducing path relative to <L,S> on an mixed-edge graph with directed and bidirected edges, where every non-endpoint vertex on p is either in L or a collider, and every collider on p is an ancestor of either X , Y or a member of S.

In other words, it is a path between two nodes that cannot be d-seperated, making it active regardless of what variables we condition on.

More details on inducing paths can be found at [1].

import pywhy_graphs
from pywhy_graphs import ADMG
from pywhy_graphs.viz import draw

Construct an example graph

To illustrate the workings of the inducing path algorithm, we will construct the causal graph from figure 2 of [2].

G = ADMG()
G.add_edge("X4", "X1", G.directed_edge_name)
G.add_edge("X2", "X5", G.directed_edge_name)
G.add_edge("X2", "X6", G.directed_edge_name)
G.add_edge("X4", "X6", G.directed_edge_name)
G.add_edge("X3", "X6", G.directed_edge_name)
G.add_edge("X3", "X4", G.directed_edge_name)
G.add_edge("X3", "X2", G.directed_edge_name)
G.add_edge("X5", "X6", G.directed_edge_name)
G.add_edge("L2", "X4", G.directed_edge_name)
G.add_edge("L2", "X5", G.directed_edge_name)
G.add_edge("L1", "X1", G.directed_edge_name)
G.add_edge("L1", "X2", G.directed_edge_name)


# this is the Figure 2(a) in the paper as we see.
dot_graph = draw(G)
dot_graph.render(outfile="graph.png", view=True)

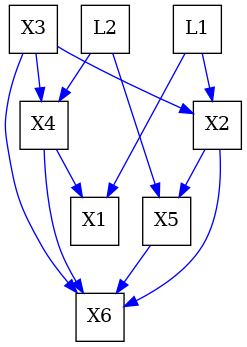
'graph.png'

Adjacent nodes trivially have an inducing path

By definition, all adjacent nodes have a trivial inducing path between them, that path only consists of one edge, which is the edge between those two nodes.

L = {}
S = {}

# All such tests will return True.
print(pywhy_graphs.inducing_path(G, "X1", "X4", L, S))
print(pywhy_graphs.inducing_path(G, "X3", "X2", L, S))

(True, ['X1', 'X4'])
(True, ['X3', 'X2'])

Inducing paths between non-adjacent nodes

Given the definition of an inducing path, we need to satisfy all requirements for the function to return True. Adding the latent variables to L is not enough for the pair [X1,X5]. As we see in Figure 2(c) in [2], (X1, X5) are not adjacent in the final skeleton of the equivalence class, which makes sense because a MAG is an equivalence class of a DAG and contains an edge among two nodes if i) the two nodes are adjacent in the DAG, or ii) the two nodes have a primitive inducing path between them. Since there is no adjacency among (X1, X5) in the final skeleton, there is no primitive inducing path between them.

L = {"L1", "L2"}
S = {}


# returns False
print(pywhy_graphs.inducing_path(G, "X1", "X5", L, S))


# However, if we add X3, a non-collider on the path
# from X1 to X5 to L, we make a valid inducing path.


L = {"L1", "L2", "X3"}
S = {}

# now it returns True
print(pywhy_graphs.inducing_path(G, "X1", "X5", L, S))

(False, [])
(True, ['X1', 'L1', 'X2', 'X3', 'X4', 'L2', 'X5'])

The role of colliders

Adding colliders to the set S has a downstream effect. Conditioning on a collider, or descendant of a collider opens up that collider path. For example, we will add the node ‘X6’ to the set S. This will make the path (X1, X2, X3) a valid inducing path, since ‘X2’ is an ancestor of ‘X6’.

# Some node pairs still do not have a valid inducing path between them.
# For example, the path between X1 and X3 is not available.

# this returns False
print(pywhy_graphs.inducing_path(G, "X1", "X3", L, S))

# If we add X6 to ``S``, paths containing all the collider ancestors of X6
# will be valid inducing paths.
# Since X2 is a collider and an ancestor of X6, there should be a valid inducing
# path from X1 to X3 now.

L = {"L1", "L2", "X3"}
S = {"X6"}

# now it returns True
print(pywhy_graphs.inducing_path(G, "X1", "X3", L, S))

(False, [])
(False, [])

References

[1]

Jiji Zhang. On the completeness of orientation rules for causal discovery in the presence of latent confounders and selection bias. Artificial Intelligence, 172(16):1873–1896, 2008. URL: https://www.sciencedirect.com/science/article/pii/S0004370208001008, doi:https://doi.org/10.1016/j.artint.2008.08.001.

[2] (1,2)

Diego Colombo, Marloes H. Maathuis, Markus Kalisch, and Thomas S. Richardson. Learning high-dimensional directed acyclic graphs with latent and selection variables. The Annals of Statistics, 40(1):294 – 321, 2012. URL: https://doi.org/10.1214/11-AOS940, doi:10.1214/11-AOS940.

Estimated memory usage: 166 MB