MixedEdgeGraph - Graph with different types of edges

A MixedEdgeGraph is a graph comprised of a tuple, \(G = (V, E)\). The difference compared to the other networkx graphs are the edges, E. E is comprised of a set of mixed edges defined by the user. This allows arbitrary representation of graphs with different types of edges. The MixedEdgeGraph class represents each type of edge using an internal graph that is one of nx.Graph or nx.DiGraph classes. Each internal graph represents one type of edge.

Semantically a MixedEdgeGraph with just one type of edge, is just a normal nx.Graph` or ``nx.DiGraph and should be converted to its appropriate networkx class.

For example, causal graphs typically have two types of edges:

• -> directed edges representing causal relations

• <-> bidirected edges representing the presence of an unobserved confounder.

This would type of mixed-edge graph with two internal graphs: a nx.DiGraph to represent the directed edges, and a nx.Graph to represent the bidirected edges.

import matplotlib.pyplot as plt
import networkx as nx

import pywhy_graphs as pg

Construct a MixedEdgeGraph

Here we demonstrate how to construct a mixed edge graph by composing networkx graphs.

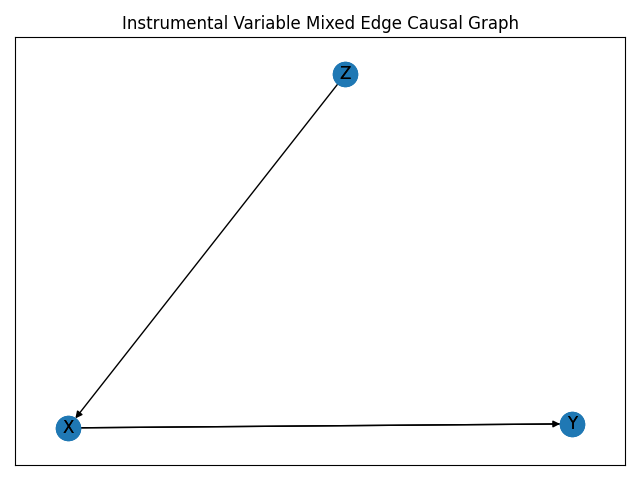
directed_G = nx.DiGraph(
    [
        ("X", "Y"),
        ("Z", "X"),
    ]
)
bidirected_G = nx.Graph(
    [
        ("X", "Y"),
    ]
)
directed_G.add_nodes_from(bidirected_G.nodes)
bidirected_G.add_nodes_from(directed_G.nodes)
G = pg.networkx.MixedEdgeGraph(
    graphs=[directed_G, bidirected_G],
    edge_types=["directed", "bidirected"],
    name="IV Graph",
)

pos = nx.spring_layout(G)

# we can then visualize the mixed-edge graph
fig, ax = plt.subplots()
nx.draw_networkx(G.get_graphs(edge_type="directed"), pos=pos, ax=ax)
nx.draw_networkx(G.get_graphs(edge_type="bidirected"), pos=pos, ax=ax)
ax.set_title("Instrumental Variable Mixed Edge Causal Graph")
fig.tight_layout()
plt.show(block=False)

Mixed Edge Graph Properties

print(G.name)

# G is directed since there are directed edges
print(f"{G} is directed: {G.is_directed()} because there are directed edges.")

# MixedEdgeGraphs are not multigraphs
print(G.is_multigraph())

# the different edge types present in the graph
print(G.edge_types)

# the internal networkx graphs representing each edge type
print(G.get_graphs())

# we can specifically get the networkx graph representation
# of any edge, e.g. the bidirected edges
bidirected_edges = G.get_graphs("bidirected")

IV Graph
MixedEdgeGraph named 'IV Graph' with 3 nodes and 3 edges and 2 edge types is directed: False because there are directed edges.
False
['directed', 'bidirected']
{'directed': <networkx.classes.digraph.DiGraph object at 0x7f25cc781510>, 'bidirected': <networkx.classes.graph.Graph object at 0x7f25de451590>}

Mixed Edge Graph Operations on Nodes

# Nodes: Similar to ``nx.Graph`` and ``nx.DiGraph``, the nodes of the graph
# can be queried via the same API. By default nodes are stored
# inside every internal graph.
nodes = G.nodes
assert G.order() == len(G)
assert len(G) == G.number_of_nodes()
print(f"{G} has nodes: {nodes}")

# If we add a node, then we can query if the new node is there
print(f"Graph has node A: {G.has_node('A')}")
G.add_node("A")
print(f"Now graph has node A: {G.has_node('A')}")

# Now, we can remove the node
G.remove_node("A")
print(f"Graph has node A: {G.has_node('A')}")

MixedEdgeGraph named 'IV Graph' with 3 nodes and 3 edges and 2 edge types has nodes: ['X', 'Y', 'Z']
Graph has node A: False
Now graph has node A: True
Graph has node A: False

Mixed Edge Graph Operations on Edges

Mixed edge graphs are just like normal networkx graph classes, except that they store an internal networkx graph per edge type. As a result, each edge now corresponds to an ‘edge_type’, which typically must be specified in edge operations for mixed edge graphs.

# Edges: We can query specific edges by type
print(f"The graph has directed edges: {G.edges()['directed']}")

# Note these edges correspond to the edges of the internal networkx
# DiGraph that represents the directed edges
print(G.get_graphs("directed").edges())

# When querying, adding, or removing an edge, you must specify
# the edge type as well.
# Here, we can add a new Z <-> Y bidirected edge.
assert G.has_edge("X", "Y", edge_type="directed")
G.add_edge("Z", "Y", edge_type="bidirected")
assert not G.has_edge("Z", "Y", edge_type="directed")

# Now, we can remove the Z <-> Y bidirected edge.
G.remove_edge("Z", "Y", edge_type="bidirected")
assert not G.has_edge("Z", "Y", edge_type="bidirected")

The graph has directed edges: [('X', 'Y'), ('Z', 'X')]
[('X', 'Y'), ('Z', 'X')]

Mixed Edge Graph Key Differences

Mixed edge graphs implement the standard networkx API, but the adj, edges, and degree are functions instead of class properties. Moreover, one can specify the edge type.

# Neighbors: Compared to its uni-edge networkx counterparts, a mixed-edge
# graph has many edge types. We define neighbors as any node with a connection.
# This is similar to `nx.Graph` where neighbors are any adjacent neighbors.
assert "Z" in G.neighbors("X")

# Similar to the networkx API, the ``adj`` provides a way to iterate
# through the nodes and edges, but now over different edge types.
for edge_type, adj in G.adj.items():
    print(edge_type)
    print(adj)

# If you only want the adjacencies of the directed edges, you can
# query the returned dictionary of adjacencies.
print(G.adj["directed"])

# Similar to the networkx API, the ``edges`` provides a way to iterate
# through the edges, but now over different edge types.
for edge_type, edges in G.edges().items():
    print(edge_type)
    print(edges)

# Similar to the networkx API, the ``edges`` provides a way to iterate
# through the edges, but now over different edge types.
for node, degrees in G.degree().items():
    print(f"{node} with degree: {degrees}")

directed
{'X': {'Y': {}}, 'Y': {}, 'Z': {'X': {}}}
bidirected
{'X': {'Y': {}}, 'Y': {'X': {}}, 'Z': {}}
{'X': {'Y': {}}, 'Y': {}, 'Z': {'X': {}}}
directed
[('X', 'Y'), ('Z', 'X')]
bidirected
[('X', 'Y')]
directed with degree: [('X', 2), ('Y', 1), ('Z', 1)]
bidirected with degree: [('X', 1), ('Y', 1), ('Z', 0)]

Estimated memory usage: 172 MB