pywhy_graphs.PAG#

class pywhy_graphs.PAG(incoming_directed_edges=None, incoming_undirected_edges=None, incoming_bidirected_edges=None, incoming_circle_edges=None, directed_edge_name: str = 'directed', undirected_edge_name: str = 'undirected', bidirected_edge_name: str = 'bidirected', circle_edge_name: str = 'circle', **attr)[source]#

Partial ancestral graph (PAG).

PAGs are a Markov equivalence class with mixed edges of directed, bidirected, undirected and edges with circle endpoints. In terms of graph functionality, they essentially extend the definition of an ADMG with edges with circular endpoints.

Parameters:

incoming_directed_edgesinput directed edges (optional, default: None): Data to initialize directed edges. All arguments that are accepted by networkx.DiGraph are accepted.
incoming_undirected_edgesinput undirected edges (optional, default: None): Data to initialize undirected edges. All arguments that are accepted by networkx.Graph are accepted.
incoming_bidirected_edgesinput bidirected edges (optional, default: None): Data to initialize bidirected edges. All arguments that are accepted by networkx.Graph are accepted.
incoming_circle_edgesinput circular endpoint edges (optional, default: None): Data to initialize edges with circle endpoints. All arguments that are accepted by networkx.DiGraph are accepted.
directed_edge_namestr: The name for the directed edges. By default ‘directed’.
undirected_edge_namestr: The name for the undirected edges. By default ‘undirected’.
bidirected_edge_namestr: The name for the bidirected edges. By default ‘bidirected’.
circle_edge_namestr: The name for the circle edges. By default ‘circle’.
attrkeyword arguments, optional (default= no attributes): Attributes to add to graph as key=value pairs.

See also

networkx.DiGraph
networkx.Graph
pywhy_graphs.ADMG
pywhy_graphs.networkx.MixedEdgeGraph

Notes

PAGs are Markov equivalence class of causal ADMGs. The implicit assumption in these causal graphs are the Structural Causal Model (or SCM) is Semi-Markovian, such that latent confounders may be present. This allows PAGs to be learned from constraint-based (such as the FCI algorithm) approaches for causal structure learning.

Edge Type Subgraphs

The data structure underneath the hood is stored in two types of networkx graphs: networkx.Graph and networkx.DiGraph.

Directed edges (<-, ->, indicating causal relationship) = networkx.DiGraph
The subgraph of directed edges may be accessed by the ~.PAG.sub_directed_graph. Their edges in networkx format can be accessed by directed_edges and the corresponding name of the edge type by directed_edge_name.
Bidirected edges (<->, indicating latent confounder) = networkx.Graph
The subgraph of bidirected edges may be accessed by the ~.PAG.sub_bidirected_graph. Their edges in networkx format can be accessed by bidirected_edges and the corresponding name of the edge type by bidirected_edge_name.
Undirected edges (–, indicating selection bias) = networkx.Graph
The subgraph of undirected edges may be accessed by the ~.PAG.sub_undirected_graph. Their edges in networkx format can be accessed by ~.PAG.undirected_edges and the corresponding name of the edge type by ~.PAG.undirected_edge_name.
Circle edges (-o, o-, indicating uncertainty) = networkx.DiGraph
The subgraph of undirected edges may be accessed by the ~.PAG.sub_circle_graph. Their edges in networkx format can be accessed by ~.PAG.circle_edges and the corresponding name of the edge type by ~.PAG.circle_edge_name.

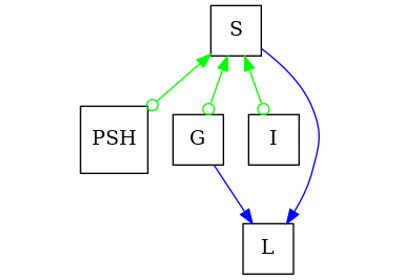
How different edges are represented in the PAG

Compared to an ~pywhy_graphs.classes.ADMG and ~pywhy_graphs.classes.CPDAG and a networkx.DiGraph, a PAG is more complex in that it generalizes endpoints an edge can take, exponentially increasing the number of possible edges that can occur between two nodes. The main complication arises in edges with circle endpoints. Rather than store all possible edges as separate networkx graphs, we have a set of rules that map a combination of the above edge-type subgraphs to a certain edge.

Bidirected and undirected edges are represented by one networkx graph (networkx.Graph). They are simple in that they do not require pairing with another edge-type subgraph.

x <-> y: is a bidirected edge present? (Note by definition of a PAG no other edge
can be present between x and y)
x - y: is an undirected present? (Note no other edge should be present in any
other direction, so an undirected edge is similar to a bidirected edge in that it represents only one kind of edge)

Edges with arrowheads, tails and circular endpoints are represented by another networkx graph (networkx.DiGraph). They complicate matters because the ~.PAG.sub_directed_graph and ~.PAG.sub_circle_graph can be combined in different ways to result in different edges between x and y.

Without loss of generality, we will be dealing with the ordered tuple (x, y). If you want the other direction of the edge, you can just flip the order of x and y. For example, x <- y would just be y -> x, so we will only discuss the -> edge. The following rules dictate what sort of edge we are dealing with:

x o-o y: is circle edge present in both directions? There are only edges present
in the ~.PAG.sub_circle_graph between x and y.
x o-> y: is circle edge one way and directed edge another way? There is an edge from
the ~.PAG.sub_circle_graph and the ~.PAG.sub_directed_graph between x and y in opposite directions.
x o- y: is there only one circle edge? In this special case, we do not use the
~.PAG.sub_undirected_graph to represent the tail endpoint at y. There is only one edge in the ~.PAG.sub_circle_graph between x and y.

add_edge(u_of_edge, v_of_edge, edge_type='all', **attr)[source]#

Add an edge between u and v.

The nodes u and v will be automatically added if they are not already in the graph.

Edge attributes can be specified with keywords or by directly accessing the edge’s attribute dictionary.

Parameters:

u_for_edge, v_for_edgenodes: Nodes can be, for example, strings or numbers. Nodes must be hashable (and not None) Python objects.
edge_typestr: The edge type. By default ‘all’, which will then add an edge in all edge type subgraphs.
attrkeyword arguments, optional: Edge data (or labels or objects) can be assigned using keyword arguments.

See also

add_edges_from: add a collection of edges

add_edges_from(ebunch_to_add, edge_type, **attr)[source]#

Add all the edges in ebunch_to_add.

Parameters:

ebunch_to_addcontainer of edges: Each edge given in the container will be added to the graph. The edges must be given as 2-tuples (u, v) or 3-tuples (u, v, d) where d is a dictionary containing edge data.
edge_typestr: The edge type to add edges to. By default ‘all’, which will then add an edge in all edge type subgraphs.
attrkeyword arguments, optional: Edge data (or labels or objects) can be assigned using keyword arguments.

See also

add_edge: add a single edge

Notes

Adding the same edge twice has no effect but any edge data will be updated when each duplicate edge is added.

Edge attributes specified in an ebunch take precedence over attributes specified via keyword arguments.

children(n: int | float | str | Any) → Iterator[source]#

Return the definite children of node ‘n’ in a PAG.

Definite children are children of node ‘n’ with only a directed edge between them from ‘n’ -> ‘x’. For example, ‘n’ o-> ‘x’ does not qualify ‘x’ as a children of ‘n’.

Parameters:

nnode: A node in the causal DAG.

Yields:

childrenIterator: An iterator of the children of node ‘n’.

See also

possible_children
parents
possible_parents

property circle_edge_name: str#: Name of the circle edge subgraph.

property circle_edges: Mapping#: EdgeView of the circle edges.

Orient undirected edge into an arrowhead.

If there is an undirected edge u - v, then the arrowhead will orient u -> v. If the correct order is v <- u, then simply pass the arguments in different order.

Parameters:

unode: The parent node
vnode: The node that ‘u’ points to in the graph.

parents(n: int | float | str | Any) → Iterator[source]#

Return the definite parents of node ‘n’ in a PAG.

Definite parents are parents of node ‘n’ with only a directed edge between them from ‘n’ <- ‘x’. For example, ‘n’ <-o ‘x’ does not qualify ‘x’ as a parent of ‘n’.

Parameters: