Estimating effect of multiple treatments
[1]:
from dowhy import CausalModel
import dowhy.datasets
import warnings
warnings.filterwarnings('ignore')
[2]:
data = dowhy.datasets.linear_dataset(10, num_common_causes=4, num_samples=10000,
num_instruments=0, num_effect_modifiers=2,
num_treatments=2,
treatment_is_binary=False,
num_discrete_common_causes=2,
num_discrete_effect_modifiers=0,
one_hot_encode=False)
df=data['df']
df.head()
[2]:
| X0 | X1 | W0 | W1 | W2 | W3 | v0 | v1 | y | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 3.478355 | 0.950201 | -1.283866 | 0.702492 | 2 | 2 | 15.825919 | 4.221690 | 969.126674 |
| 1 | 0.111915 | 0.533298 | 1.928152 | 0.362418 | 2 | 0 | 17.018736 | 10.067362 | 502.977712 |
| 2 | 1.028958 | 0.553118 | 3.040734 | 1.852888 | 0 | 2 | 24.175454 | 17.575311 | 2084.692456 |
| 3 | 0.761331 | 0.986196 | 1.466116 | 0.484399 | 0 | 1 | 13.621585 | 6.120504 | 534.611529 |
| 4 | 0.565970 | -0.298851 | 1.782537 | 0.553373 | 1 | 3 | 25.190648 | 10.968219 | 673.748567 |
[3]:
model = CausalModel(data=data["df"],
treatment=data["treatment_name"], outcome=data["outcome_name"],
graph=data["gml_graph"])
[4]:
model.view_model()
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
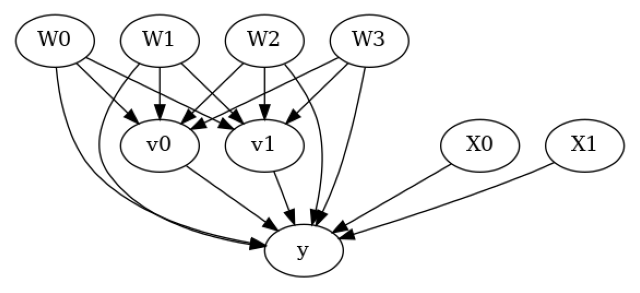
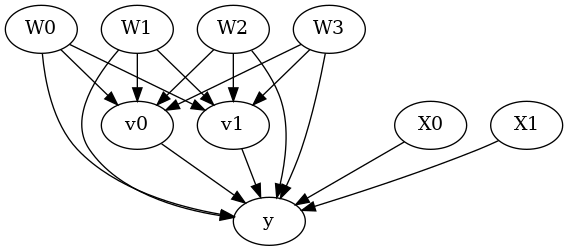
[5]:
identified_estimand= model.identify_effect(proceed_when_unidentifiable=True)
print(identified_estimand)
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────────(E[y|W3,W2,W1,W0])
d[v₀ v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W3,W2,W1,W0,U) = P(y|v0,v1,W3,W2,W1,W0)
### Estimand : 2
Estimand name: iv
No such variable(s) found!
### Estimand : 3
Estimand name: frontdoor
No such variable(s) found!
Linear model
Let us first see an example for a linear model. The control_value and treatment_value can be provided as a tuple/list when the treatment is multi-dimensional.
The interpretation is change in y when v0 and v1 are changed from (0,0) to (1,1).
[6]:
linear_estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.linear_regression",
control_value=(0,0),
treatment_value=(1,1),
method_params={'need_conditional_estimates': False})
print(linear_estimate)
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────────(E[y|W3,W2,W1,W0])
d[v₀ v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W3,W2,W1,W0,U) = P(y|v0,v1,W3,W2,W1,W0)
## Realized estimand
b: y~v0+v1+W3+W2+W1+W0+v0*X1+v0*X0+v1*X1+v1*X0
Target units: ate
## Estimate
Mean value: 130.27662853752327
You can estimate conditional effects, based on effect modifiers.
[7]:
linear_estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.linear_regression",
control_value=(0,0),
treatment_value=(1,1))
print(linear_estimate)
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────────(E[y|W3,W2,W1,W0])
d[v₀ v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W3,W2,W1,W0,U) = P(y|v0,v1,W3,W2,W1,W0)
## Realized estimand
b: y~v0+v1+W3+W2+W1+W0+v0*X1+v0*X0+v1*X1+v1*X0
Target units:
## Estimate
Mean value: 130.27662853752327
### Conditional Estimates
__categorical__X1 __categorical__X0
(-4.093, 0.0588] (-3.53, 0.0899] 2.090685
(0.0899, 0.665] 51.194647
(0.665, 1.173] 78.741560
(1.173, 1.753] 107.293791
(1.753, 4.508] 155.951323
(0.0588, 0.64] (-3.53, 0.0899] 33.311782
(0.0899, 0.665] 81.214917
(0.665, 1.173] 110.623183
(1.173, 1.753] 140.540786
(1.753, 4.508] 190.205985
(0.64, 1.162] (-3.53, 0.0899] 51.899674
(0.0899, 0.665] 100.666380
(0.665, 1.173] 131.176068
(1.173, 1.753] 160.418091
(1.753, 4.508] 209.396845
(1.162, 1.749] (-3.53, 0.0899] 70.789839
(0.0899, 0.665] 119.822565
(0.665, 1.173] 149.082664
(1.173, 1.753] 178.997122
(1.753, 4.508] 230.296951
(1.749, 4.594] (-3.53, 0.0899] 102.942682
(0.0899, 0.665] 150.433502
(0.665, 1.173] 179.368204
(1.173, 1.753] 211.821964
(1.753, 4.508] 258.463569
dtype: float64
More methods
You can also use methods from EconML or CausalML libraries that support multiple treatments. You can look at examples from the conditional effect notebook: https://py-why.github.io/dowhy/example_notebooks/dowhy-conditional-treatment-effects.html
Propensity-based methods do not support multiple treatments currently.