Mediation analysis with DoWhy: Direct and Indirect Effects

import numpy as np
import pandas as pd

from dowhy import CausalModel
import dowhy.datasets

# Warnings and logging
import warnings
warnings.filterwarnings('ignore')

Creating a dataset

# Creating a dataset with a single confounder and a single mediator (num_frontdoor_variables)
data = dowhy.datasets.linear_dataset(10, num_common_causes=1, num_samples=10000,
                                     num_instruments=0, num_effect_modifiers=0,
                                     num_treatments=1,
                                     num_frontdoor_variables=1,
                                     treatment_is_binary=False,
                                    outcome_is_binary=False)
df = data['df']
print(df.head())

         FD0        W0        v0          y
0  -6.447555 -0.075789 -1.077450  -8.042200
1 -21.868899 -0.928403 -4.153001 -28.356976
2 -34.539353 -1.541724 -7.257781 -44.899791
3   6.394029  0.394910  1.259933   8.491919
4  25.905142  0.901329  5.415971  33.246344

Step 1: Modeling the causal mechanism

We create a dataset following a causal graph based on the frontdoor criterion. That is, there is no direct effect of the treatment on outcome; all effect is mediated through the frontdoor variable FD0.

model = CausalModel(df,
                    data["treatment_name"],data["outcome_name"],
                    data["gml_graph"],
                   missing_nodes_as_confounders=True)

model.view_model()
from IPython.display import Image, display
display(Image(filename="causal_model.png"))

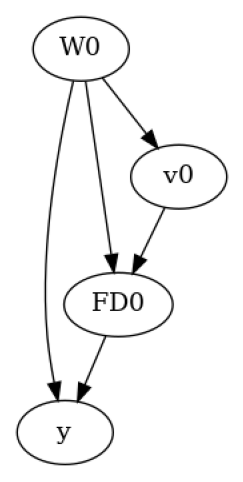
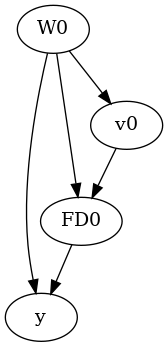
Step 2: Identifying the natural direct and indirect effects

We use the estimand_type argument to specify that the target estimand should be for a natural direct effect or the natural indirect effect. For definitions, see Interpretation and Identification of Causal Mediation by Judea Pearl.

Natural direct effect: Effect due to the path v0->y

Natural indirect effect: Effect due to the path v0->FD0->y (mediated by FD0).

# Natural direct effect (nde)
identified_estimand_nde = model.identify_effect(estimand_type="nonparametric-nde",
                                            proceed_when_unidentifiable=True)
print(identified_estimand_nde)

Estimand type: EstimandType.NONPARAMETRIC_NDE

### Estimand : 1
Estimand name: mediation
Estimand expression:
 ⎡  d         ⎤
E⎢─────(y|FD0)⎥
 ⎣d[v₀]       ⎦
Estimand assumption 1, Mediation: FD0 intercepts (blocks) all directed paths from v0 to y except the path {v0}→{y}.
Estimand assumption 2, First-stage-unconfoundedness: If U→{v0} and U→{FD0} then P(FD0|v0,U) = P(FD0|v0)
Estimand assumption 3, Second-stage-unconfoundedness: If U→{FD0} and U→y then P(y|FD0, v0, U) = P(y|FD0, v0)

# Natural indirect effect (nie)
identified_estimand_nie = model.identify_effect(estimand_type="nonparametric-nie",
                                            proceed_when_unidentifiable=True)
print(identified_estimand_nie)

Estimand type: EstimandType.NONPARAMETRIC_NIE

### Estimand : 1
Estimand name: mediation
Estimand expression:
 ⎡  d         d         ⎤
E⎢──────(y)⋅─────([FD₀])⎥
 ⎣d[FD₀]    d[v₀]       ⎦
Estimand assumption 1, Mediation: FD0 intercepts (blocks) all directed paths from v0 to y except the path {v0}→{y}.
Estimand assumption 2, First-stage-unconfoundedness: If U→{v0} and U→{FD0} then P(FD0|v0,U) = P(FD0|v0)
Estimand assumption 3, Second-stage-unconfoundedness: If U→{FD0} and U→y then P(y|FD0, v0, U) = P(y|FD0, v0)

Step 3: Estimation of the effect

Currently only two stage linear regression is supported for estimation. We plan to add a non-parametric Monte Carlo method soon as described in Imai, Keele and Yamamoto (2010).

Natural Indirect Effect

The estimator converts the mediation effect estimation to a series of backdoor effect estimations. 1. The first-stage model estimates the effect from treatment (v0) to the mediator (FD0). 2. The second-stage model estimates the effect from mediator (FD0) to the outcome (Y).

import dowhy.causal_estimators.linear_regression_estimator
causal_estimate_nie = model.estimate_effect(identified_estimand_nie,
                                        method_name="mediation.two_stage_regression",
                                       confidence_intervals=False,
                                       test_significance=False,
                                        method_params = {
                                            'first_stage_model': dowhy.causal_estimators.linear_regression_estimator.LinearRegressionEstimator,
                                            'second_stage_model': dowhy.causal_estimators.linear_regression_estimator.LinearRegressionEstimator
                                        }
                                       )
print(causal_estimate_nie)

*** Causal Estimate ***

## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_NIE

### Estimand : 1
Estimand name: mediation
Estimand expression:
 ⎡  d         d         ⎤
E⎢──────(y)⋅─────([FD₀])⎥
 ⎣d[FD₀]    d[v₀]       ⎦
Estimand assumption 1, Mediation: FD0 intercepts (blocks) all directed paths from v0 to y except the path {v0}→{y}.
Estimand assumption 2, First-stage-unconfoundedness: If U→{v0} and U→{FD0} then P(FD0|v0,U) = P(FD0|v0)
Estimand assumption 3, Second-stage-unconfoundedness: If U→{FD0} and U→y then P(y|FD0, v0, U) = P(y|FD0, v0)

## Realized estimand
(b: FD0~v0+W0)*(b: y~FD0+W0)
Target units: ate

## Estimate
Mean value: 5.903111653218544

Note that the value equals the true value of the natural indirect effect (up to random noise).

print(causal_estimate_nie.value, data["ate"])

5.903111653218544 5.9192853651707065

The parameter is called ate because in the simulated dataset, the direct effect is set to be zero.

Natural Direct Effect

Now let us check whether the direct effect estimator returns the (correct) estimate of zero.

causal_estimate_nde = model.estimate_effect(identified_estimand_nde,
                                        method_name="mediation.two_stage_regression",
                                       confidence_intervals=False,
                                       test_significance=False,
                                        method_params = {
                                            'first_stage_model': dowhy.causal_estimators.linear_regression_estimator.LinearRegressionEstimator,
                                            'second_stage_model': dowhy.causal_estimators.linear_regression_estimator.LinearRegressionEstimator
                                        }
                                       )
print(causal_estimate_nde)

*** Causal Estimate ***

## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_NDE

### Estimand : 1
Estimand name: mediation
Estimand expression:
 ⎡  d         ⎤
E⎢─────(y|FD0)⎥
 ⎣d[v₀]       ⎦
Estimand assumption 1, Mediation: FD0 intercepts (blocks) all directed paths from v0 to y except the path {v0}→{y}.
Estimand assumption 2, First-stage-unconfoundedness: If U→{v0} and U→{FD0} then P(FD0|v0,U) = P(FD0|v0)
Estimand assumption 3, Second-stage-unconfoundedness: If U→{FD0} and U→y then P(y|FD0, v0, U) = P(y|FD0, v0)

## Realized estimand
(b: y~v0+W0) - ((b: FD0~v0+W0)*(b: y~FD0+W0))
Target units: ate

## Estimate
Mean value: 2.2791967078106268e-06

Step 4: Refutations

TODO