Demo for the DoWhy causal API

We show a simple example of adding a causal extension to any dataframe.

import dowhy.datasets
import dowhy.api
from dowhy.graph import build_graph_from_str

import numpy as np
import pandas as pd

from statsmodels.api import OLS

data = dowhy.datasets.linear_dataset(beta=5,
        num_common_causes=1,
        num_instruments = 0,
        num_samples=1000,
        treatment_is_binary=True)
df = data['df']
df['y'] = df['y'] + np.random.normal(size=len(df)) # Adding noise to data. Without noise, the variance in Y|X, Z is zero, and mcmc fails.
nx_graph = build_graph_from_str(data["dot_graph"])

treatment= data["treatment_name"][0]
outcome = data["outcome_name"][0]
common_cause = data["common_causes_names"][0]
df

	W0	v0	y
0	-1.092232	False	-1.467122
1	-0.553488	True	5.092333
2	-2.721292	False	0.557821
3	-0.860433	False	-0.864048
4	-1.078330	True	3.316149
...	...	...	...
995	-1.934879	False	-0.464891
996	-0.240524	False	-0.196877
997	-1.365115	False	1.737968
998	-1.312072	False	-0.211613
999	-2.285569	False	-2.284761

1000 rows × 3 columns

# data['df'] is just a regular pandas.DataFrame
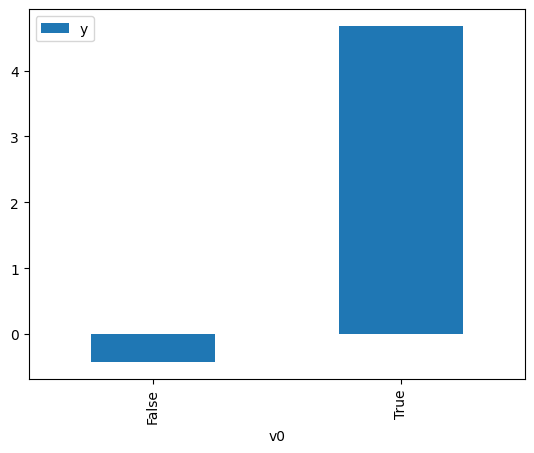
df.causal.do(x=treatment,
             variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
             outcome=outcome,
             common_causes=[common_cause],
            ).groupby(treatment).mean().plot(y=outcome, kind='bar')

<Axes: xlabel='v0'>

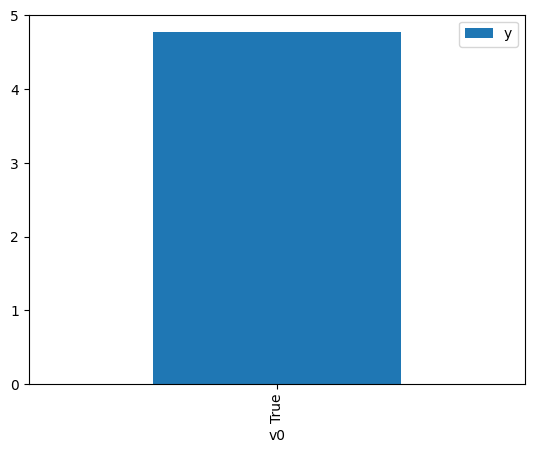
df.causal.do(x={treatment: 1},
              variable_types={treatment:'b', outcome: 'c', common_cause: 'c'},
              outcome=outcome,
              method='weighting',
              common_causes=[common_cause]
              ).groupby(treatment).mean().plot(y=outcome, kind='bar')

<Axes: xlabel='v0'>

cdf_1 = df.causal.do(x={treatment: 1},
              variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
              outcome=outcome,
              graph=nx_graph
              )

cdf_0 = df.causal.do(x={treatment: 0},
              variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
              outcome=outcome,
              graph=nx_graph
              )

cdf_0

	W0	v0	y	propensity_score	weight
0	-0.762795	False	-1.106836	0.741823	1.348030
1	-0.639424	False	-1.569639	0.713176	1.402178
2	0.270371	False	0.446674	0.461197	2.168270
3	-1.889006	False	0.264200	0.914941	1.092967
4	-0.732039	False	0.578589	0.734859	1.360806
...	...	...	...	...	...
995	-2.200991	False	1.705738	0.939414	1.064493
996	0.338915	False	-0.224639	0.441305	2.266005
997	-0.556969	False	-0.198539	0.693007	1.442988
998	-1.732231	False	0.170568	0.899507	1.111720
999	-0.504828	False	-0.317645	0.679853	1.470905

1000 rows × 5 columns

cdf_1

	W0	v0	y	propensity_score	weight
0	-0.687302	True	3.268349	0.275483	3.629985
1	-1.452541	True	5.436494	0.134246	7.449006
2	-0.978979	True	4.749862	0.212678	4.701941
3	-0.397370	True	5.544810	0.348158	2.872257
4	0.406560	True	5.071772	0.578143	1.729677
...	...	...	...	...	...
995	-0.943522	True	5.675177	0.219720	4.551243
996	-1.128276	True	6.212309	0.184846	5.409895
997	0.130132	True	6.075339	0.497787	2.008891
998	0.092802	True	4.321617	0.486851	2.054015
999	-0.357319	True	4.093820	0.358886	2.786397

1000 rows × 5 columns

Comparing the estimate to Linear Regression

First, estimating the effect using the causal data frame, and the 95% confidence interval.

(cdf_1['y'] - cdf_0['y']).mean()

$\displaystyle 5.00588480884916$

1.96*(cdf_1['y'] - cdf_0['y']).std() / np.sqrt(len(df))

$\displaystyle 0.0885944212046903$

Comparing to the estimate from OLS.

model = OLS(np.asarray(df[outcome]), np.asarray(df[[common_cause, treatment]], dtype=np.float64))
result = model.fit()
result.summary()

OLS Regression Results

Dep. Variable:	y	R-squared (uncentered):	0.906
Model:	OLS	Adj. R-squared (uncentered):	0.906
Method:	Least Squares	F-statistic:	4820.
Date:	Mon, 21 Apr 2025	Prob (F-statistic):	0.00
Time:	07:38:51	Log-Likelihood:	-1406.3
No. Observations:	1000	AIC:	2817.
Df Residuals:	998	BIC:	2826.
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
x1	0.0705	0.029	2.444	0.015	0.014	0.127
x2	4.9838	0.051	97.384	0.000	4.883	5.084

Omnibus:	2.579	Durbin-Watson:	2.017
Prob(Omnibus):	0.275	Jarque-Bera (JB):	2.490
Skew:	0.075	Prob(JB):	0.288
Kurtosis:	2.808	Cond. No.	1.79

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.