Customizing Causal Mechanism Assignment

In GCM-based inference, fitting means, we learn the generative model of the variables in the graph from data. Before we can fit the variables to data, each node in a causal graph requires a generative causal model, or a “causal mechanism”. In this section, we’ll dive deeper into how to use this feature.

To understand this, let’s pull up the mental model for a probabilistic causal model (PCM) again:

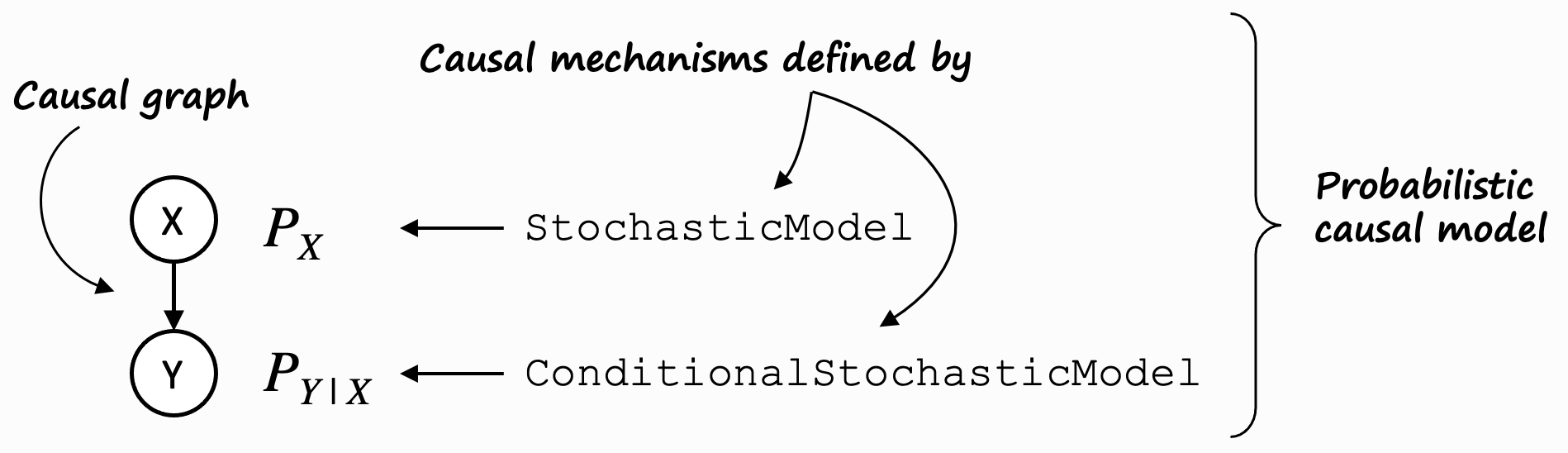
On the left, it shows a trivial causal graph \(X \rightarrow Y\). \(X\) is a so-called root node (it has no parents), \(Y\) is a non-root node (it has parents). We fundamentally distinguishes between these two types of nodes.

For root nodes such as \(X\), the distribution \(P_x\) is modeled using a stochastic model. Non-root nodes such as \(Y\) are modelled using a conditional stochastic model. DoWhy’s gcm package defines corresponding interfaces for both, namely StochasticModel and ConditionalStochasticModel.

The gcm package also provides ready-to-use implementations, such as ScipyDistribution or BayesianGaussianMixtureDistribution for StochasticModel, and AdditiveNoiseModel for ConditionalStochasticModel.

Knowing that, we can now start to manually assign causal models to nodes according to our needs. Say, we know from domain knowledge, that our root node X follows a normal distribution. In this case, we can explicitly assign this:

>>> from scipy.stats import norm
>>> import networkx as nx
>>> from dowhy import gcm
>>>
>>> causal_model = gcm.ProbabilisticCausalModel(nx.DiGraph([('X', 'Y')]))
>>> causal_model.set_causal_mechanism('X', gcm.ScipyDistribution(norm))

For the non-root node Y, let’s use an additive noise model (ANM), represented by the AdditiveNoiseModel class. It has a structural assignment of the form: \(Y := f(X) + N\). Here, f is a deterministic prediction function, whereas N is a noise term. Let’s put all of this together:

>>> causal_model.set_causal_mechanism('Y',
>>>                                   gcm.AdditiveNoiseModel(prediction_model=gcm.ml.create_linear_regressor(),
>>>                                                          noise_model=gcm.ScipyDistribution(norm)))

The rather interesting part here is the prediction_model, which corresponds to our function \(f\) above. This prediction model must satisfy the contract defined by PredictionModel, i.e. it must implement the methods:

def fit(self, X: np.ndarray, Y: np.ndarray) -> None: ...
def predict(self, X: np.ndarray) -> np.ndarray: ...

This interface is very analogous to model interfaces in many machine learning libraries, such as Scikit Learn. In fact the gcm package provides multiple adapter classes to make libraries such as Scikit Learn interoperable.

Now that we have associated a data-generating process to each node in the causal graph, let us prepare the training data.

>>> import numpy as np, pandas as pd
>>> X = np.random.normal(loc=0, scale=1, size=1000)
>>> Y = 2*X + np.random.normal(loc=0, scale=1, size=1000)
>>> data = pd.DataFrame(data=dict(X=X, Y=Y))

Finally, we can learn the parameters of those causal models from the training data.

>>> gcm.fit(causal_model, data)

causal_model is now ready to be used for various types of causal queries as explained in Performing Causal Tasks.

Note

As mentioned above, DoWhy has a wrapper class that supports scikit learn models out of the box. For instance

>>> from sklearn.ensemble import RandomForestRegressor
>>> causal_model.set_causal_mechanism('Y', gcm.AdditiveNoiseModel(gcm.ml.SklearnRegressionModel(RandomForestRegressor)))

would use a RandomForestRegressor instead of a LinearRegressor from the sklearn package.

Using ground truth models

In some scenarios the ground truth models might be known and should be used instead. Let’s assume, we know that our relationship are linear with coefficients \(\alpha = 2\) and \(\beta = 3\). Let’s make use of this knowledge by creating a custom prediction model that implements the PredictionModel interface:

>>> import dowhy.gcm.ml.prediction_model
>>>
>>> class MyCustomModel(gcm.ml.PredictionModel):
>>>     def __init__(self, coefficient):
>>>         self.coefficient = coefficient
>>>
>>>     def fit(self, X, Y):
>>>         # Nothing to fit here, since we know the ground truth.
>>>         pass
>>>
>>>     def predict(self, X):
>>>         return self.coefficient * X
>>>
>>>     def clone(self):
>>>         return MyCustomModel(self.coefficient)

Now we can use this in our ANMs instead:

>>> causal_model.set_causal_mechanism('Y', gcm.AdditiveNoiseModel(MyCustomModel(2)))
>>> gcm.fit(causal_model, data)

Note

Important: When a function or algorithm is called that requires a causal graph, DoWhy GCM sorts the input features internally based on their alphabetical order. For instance, in case of the MyCustomModel above, if the names of the input features are ‘X2’ and ‘X1’, the model should expect ‘X1’ in the first input and ‘X2’ in the second column.

Creating causal model (GCM) from equations

In the above section, we saw how ground truth models can be created and used for a node. Now in cases where we know the ground truth for almost all of the nodes and we want to create a custom causal model out of it without writing a lot of code. That is when creating a graphical causal model (GCM) from equations serves as a robust utility, enabling the generation of a causal model by defining relationships between nodes. This functionality proves highly valuable when the inter-node relationships are known, providing a means to construct a custom causal model. In this section, we’ll dive deeper into how to use this feature.

Defining Equations:

The functionality supports three equation formats: root node equation, non-root node equation, and an equation for an unknown causal relationship.
Structure for each node type:
1. Root Node
  <node_name> = \(N_i\)
2. Non-root Node
  <node_name> = \(f_i(PA_i) + N_i\)
3. Unknown relationship of node with its parent nodes
  <node_name> -> PA_i,…
Note here in the above structure, the \(N_i\) is the noise model and the \(f_i(PA_i)\) notation is the functional causal model or simply a function which defines the relationship between the current node and its parent nodes.
Root node equation defines the relationship for a root node, specifying a noise model. Non-root node equation extends this by incorporating a function expression involving other nodes and a noise model. Unknown causal model equation is used when the exact relationship between nodes is unknown, only specifying the edges.

Defining Noise Models(N):

The noise models include options like empirical, Bayesian Gaussian mixture, parametric, and those from the scipy.stats library. Lets look at each option in detail -
1. empirical(): An implementation of a stochastic model class.
2. bayesiangaussianmixture(): An implementation of a stochastic model class.
3. parametric(): Use it when you want the system to find the best continuous distribution for the data.
4. <scipy_function>(): You can specify continuous distribution functions defined in scipy.stats library.

Defining Functional Causal Models(F(X)):

Relationships between child and parent nodes can be defined in a expression which supports almost all the airthematic operations and functions under numpy library

Undefined/Unknown relationships for Nodes:

In case when the relationship between the child and parent nodes are unknown, the user can define such nodes as given below example -

\(X_i -> PA_i, PA_i\)

Example

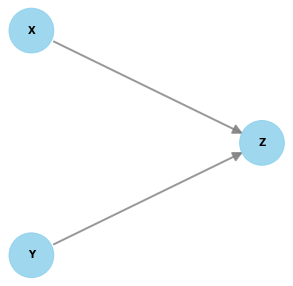
Users can provide a string containing equations representing the causal relationships between nodes.

from dowhy import gcm
from dowhy.utils import plot

scm = """
X = empirical()
Y = norm(loc=0, scale=1)
Z = 12 * X + log(abs(Y)) + norm(loc=0, scale=1)
"""
causal_model = gcm.create_causal_model_from_equations(scm)
print(plot(causal_model.graph))

Note

The functionality sanitizes the input equations to prevent security vulnerabilities.
The naming of the nodes is currently restricted to python variable naming constraints which means that the name of node can only contain alphabets, numbers (not at the start) and ‘_’ character.