Graph refutations

To test the validity of a full graph, we need to test each of the conditional independence constraints implied by the graph, known as the local Markov conditions (LMCs). To test the validity of a graph, we can write:

>>> from dowhy.gcm.falsify import falsify_graph
>>> # causal_graph is a networkx digraph
>>> result = falsify_graph(causal_graph, data, show_progress_bar=False)
>>> print(result)

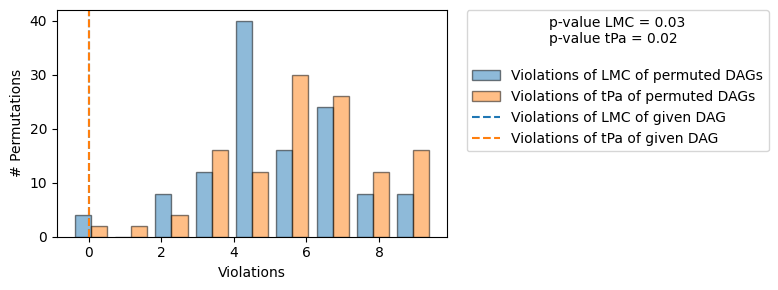
The results of falsify_graph show the output of two tests. The first measures whether the LMCs implied by the graph are satisfied by the data. It compares the number of LMCs violated by the given graph to the number of LMCs violated by random graphs. For a significance value of 0.05, if the number of LMC violations by the given graph is lower than the 5% best random graphs, then we do not reject the graph. The second test (tPa) checks whether the graph is falsifiable. That is, assuming that the given graph is correct, how many other graphs share the same number of LMC violations? Since the graph is assumed to be correct, the correct LMCs are those that are implied by the graph and hence the reference number of violations is zero. For a significance value of 0.05, if less than 5% of random graphs have zero LMC violations, then it indicates that the LMCs implied by the graph can falsify (or refute) the graph.

If we just want to find out whether a graph is falsifiable or not, we can directly query the result object.

>>> print(f"Graph is falsifiable: {result.falsifiable}, Graph is falsified: {result.falsified}")

For more details on refuting a graph using falsify_graph, check out the notebook on refuting DAGs.